우선순위 큐와 힙

우선순위 큐(priority queue)

보통의 큐는 선입선출 원칙에 의해 먼저 들어온 데이터가 먼저 나간다. 하지만 우선순위 큐는 우선순위가 높은 데이터들이 먼저 출력된다.

자료구조	삭제되는 요소
스택	가장 나중에 들어온 데이터
큐	가장 먼저 들어온 데이터
우선순위 큐	가장 우선순위가 높은 데이터

우선순위 큐의 구현 방법

배열

• 정렬되지 않은 배열: 요소를 삭제하기 복잡함
• 정렬된 배열: 요소를 삽입하기 복잡함

연결 리스트

• 정렬되지 않은 연결 리스트: 요소를 삭제하기 복잡함
• 정렬된 연결 리스트: 요소를 삽입하기 복잡함

힙

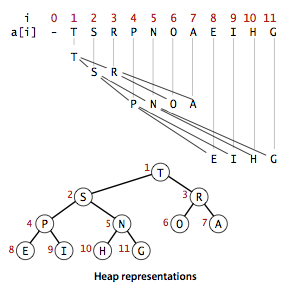
힙은 완전 이진트리의 일종으로 우선순위 큐를 위해 만들어진 자료구조이다. 힙은 일종의 반 정렬 상태를 유지한다. 자세한 건 밑에서 설명한다.

힙(heap)

힙은 부모 노드의 키 값이 자식 노드의 키 값보다 큰 완전 이진트리이다. 즉, key(A) >= key(B)인 것이다. 힙은 느슨한 정렬 상태를 유지하는데, 힙의 목적이 삭제 연산에서 가장 큰 값을 효율적으로 찾아내는 것이므로 모두 다 정렬한 필요는 없다. 참고로 힙은 이진 탐색 트리와 달리 형제 노드의 크기 관계는 상관이 없다.

최대 힙과 최소 힙

• 최대 힙(max heap): 부모 노드의 키 값이 자식 노드보다 크거나 같은 완전 이진트리
• 최소 힙(min heap): 부모 노드의 키 값이 자식 노드보다 작거나 같은 완전 이진트리

힙의 구현 방법

완전 이진트리이므로 배열을 사용한다.

배열로 표현한 힙

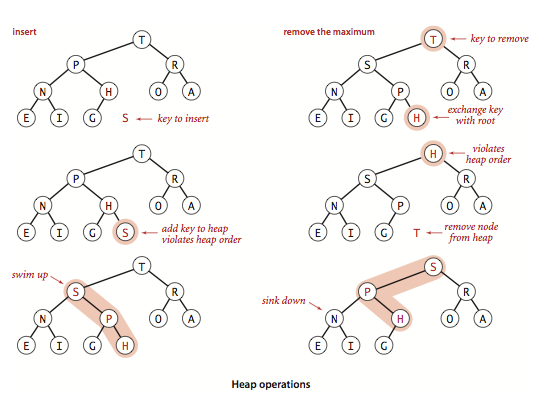
삽입

일단 마지막 노드에 삽입하고, 부모 노드들과 비교하여 위치를 조정해 나간다.

삭제

루트 노드를 삭제한 뒤, 말단 노드를 루트에 놓고 아래 노드들과의 비교를 통해 위치를 조정해 나간다.

힙의 삽입과 삭제 과정

참고로 힙은 c++의 STL 중 하나인 <queue>의 priority_queue로 쉽게 구현할 수 있다. (뭔가 주객이 전도된 거 같은데…)

시간 복잡도

삽입, 삭제 시 노드들과 값을 비교하는 과정 때문에 n개의 노드를 가진 힙은 연산 시 \(O(log_2n)\)의 시간 복잡도를 가진다.

균형 잡힌 트리의 높이가 h라면, h = \(log_2n\)이므로 n = \(2^h - 1\)이다. 따라서 높이가 h인 균형 잡힌 트리가 \(O(h)\)의 시간 복잡도를 가지면, \(O(log_2n)\)의 시간 복잡도를 갖는다.

참고

C++로 쉽게 풀어쓴 자료구조 10장
introduction to max heap
codepath
priority queue